

If you have a nearly linear dependent basis for your equations, it may help, first to search for a new orthogonalized basis, write the equation in this basis and then solve the equations.Īs an example we solve a 3D problem: Given a not orthogonal badly conditioned basis: bas and a vector v, we are searching coefficients: coef, so that coef.bas = v: b1 = *) This method can be used only if matrix A is nonsingular, thus has an inverse, and column B is not a zero vector (nonhomogeneous system). This means that to find out column vector of variables we need to multiply matrix inverse by column vector of solutions. The rank of this matrix equals 3, and so the system with four unknowns has an infinite number of. Calculator Inverse matrix calculator can be used to solve the system of linear equations. Step 2) Next, we write the 2nd variable, y in terms of z from the new equation and substitute it in the third equation. A system is solvable for n unknowns and n linear independant equations. Solves equations for up to five unknowns. A system of linear equations consists of equations of the form a 11 x 1 +a 12 x 2 +a 13 x 3 +.b 1, a 21 x 1 +a 22 x 2 +a 23 x 3 +. Find zeros of the function: f x 3 x 2 7 x 20. Functions variable: x y z t u p q s a b c.
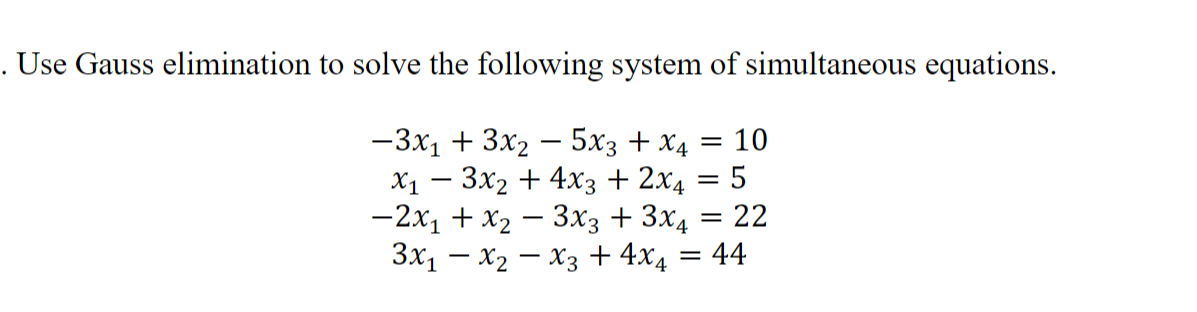
Our online calculator, based on Wolfram Alpha system is able to find zeros of almost any, even very complicated function. Solution: By elementary transformations, the coefficient matrix can be reduced to the row echelon form. Step 1) To solve a system of 2 equations with 3 variables say x, y, and z, we will consider the 1st two equations and eliminate one of the variables, say x, to obtain a new equation. Calculator for Systems of Linear Equations. Thus, the zeros of the function are at the point. Use Gaussian elimination to solve the following homogeneous system of equations. Are this equations linear ? If so you can try to transform the equations. Homogeneous Systems of Linear Equations - Examples.


 0 kommentar(er)
0 kommentar(er)
